1. The easiest thing to do here is to solve for x and plug.
Plugging 2 into the equation gives you
2. "animals" is made up of mice, cats, and dogs in this problem. The total number of animals is 2 mice + 3 cats + 6 dogs = 11 animals. The ratio of cats to animals is just 3 cats / 11 animals. 3 to 11.
3. To find angle ACB, use the property of a straight line to determine that 110 + ACB must equal 180. ACB = 70.
Since a triangle has 180 degrees, x = 180 - 40 - 70 = 70
You could also backsolve. Starting with c), x = 50, which would make ACB = 90, (180 - 40 - 50 = 90). Since we need ACB to equal 70, that's too big. Move to a higher x value, which would give you a lower ACB value. d) x = 60, ACB = 80, still too big. e) x = 70, ACB = 70. Correct.
4. Of the 12 books, 3 are sold for $5 (1 by Alex, 2 by Dana), 5 are sold for $4.50 (2 by Alex, 3 by Dana), and 4 are sold for $2.50 (4 by Alex, 0 by Dana). $4.50 is the most frequently occurring sale price.
5. Convert both to the same unit, feet. 16 yards * 3 = 48 feet. 48 - 16 = 32.
6. Find the relationship between r and s. As s goes from 4 to 9 (increasing by 5), which answer also increases by 5?
so which answer is directly proportional to s? 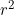
7. Plug in. As is the case with most percentage questions, plug in 100. Total customers = 100. If 20% chose black as their favorite car color, 20 out of the 100 chose black. 20 / 100 = 1 / 5
8. Vertical angles are always equal. Since RPQ = 40, TPU = 40. SPU = SPT + TPU. SPT = SPU - TPU. SPT = 70 - 40 = 30
9. f(x) = 2x. Take whatever is in the parentheses and multiply it by 2.
f(5t) = 2*5t = 10t
10. solve for expression!
ax + by = 14
+ ax - by = 4
= 2ax = 18, ax = 9
11. Equilateral triangle has equal sides. The perimeter is 18 so each side must equal 6. Because O is the center of the circle, each side of the triangle is also a radius of the circle. 2r = d. 2 * 6 = 12
12. Plug In! r = 2. 2(2) + 4 = 8 mph. At 8 mph, a car can travel 16 miles in 2 hours. e) 4r + 8 --> 4 * 2 + 8 = 16
13. Cut the figure into a rectangle and a triangle with the same base. The height of the rectangle is 4 and the base is 3. 3 * 4 = 12. The triangle has a base of 3 and a height of 6. (3 * 6) / 2 = 9. (12 + 9) = 21
14. Backsolve!
c) 10 < n =" 15." 6 =" 90" 60 =" 105">
d) n = 20. VV --> 20 * 6 = 120, GG --> 20 * 3 + 60 = 120. They're equal, but that doesn't count. GG is not cheaper.
e) n > 20. Say n = 21. VV --> 21 * 6 = 126, GG --> 21 * 3 + 60 = 123. Bingo!
15. Because triangles BCF and CDE are congruent, DE = CF = 3. CF + FE = CE --> 3 + 2 = 5. CE = BF = 5.
The area of the entire figure is the sum of the areas of the two triangles and the rectangle --> Area of triangle = 3 * 5 / 2 = 7.5. Area of rectangle = 2 * 5 = 10. 10 + 7.5 + 7.5 = 25
16. To get the largest value for one of the integers, the other 4 must be as small as possible.
Backsolve. Since this question is asking for the largest possible value, we start with e). 90 + 10 + 3 other distinct integers greater than 10, must equal 100. That is impossible since 90 + 10 is already 100, too big.
d) 10 + 84 = 94. too big
c) 10 + 64 = 74. The other 3 numbers must be 11, 12, and 13 (as small as possible while still being different and greater than 10). 74 + 11 = 85. 85 + 12 = 97. 97 + 13 = 110, too big.
b) 10 + 54 = 64. 64 + 11 + 12 + 13 = 100. Good.
OR
We know the smallest is 10. 10 + __ + __ + __ + __ = 100. Since each integer must be positive and different, the smallest combination of 4 of the 5 is:
10 + 11 + 12 + 13 + _x_ = 100. --> x = 100 - (10+11+12+13) = 54
17. Plug In! Start with x. If x = 6, y = 4, z = 3. x + y + z = 6 + 4 + 3 = 13
(x + y + z) / x = 13 / 6
18. Find the slope of the line first. m = (y1 - y0) / (x1 - x0) --> m = [(2) - (-5)] / [(3) - (/2)] = 7 / 5
To reflect each point about the line y = x means that the coordinates of each point would switch. Point A would become (-5, -2) and Point B would become (2, 3). The slope of that line would simply be the reciprocal of the original line. m = 5 / 7.
19. Plug In! Start with x. Choose a number that would make the equation easy to work with. In this case, it would be x =√5. This would make y = 1. 5(1) = (√5)(√5).
so (1)√5 / (5)√5 = 1/5
20. We need to isolate the # of popcorn containers sold. To do that, subtract the top line (popcorn + soda) from the bottom (just soda).
a) 3 | b) 4 | c) 5 | d) 6 | e) 7 | |
Change in popcorn & soda | 325 – 275 = 50 | 350 – 325 = 25 | 375 – 350 = 25 | 325 – 375 = -50 | 375 – 325 = 50 |
Change in just soda | 225 – 175 = 50 | 225 – 150 = -75 | 150 – 150 = 0 | 200 – 150 = 50 | 225 – 200 = 25 |
Change in popcorn | 50 – 50 = 0 | 25 + -75 = 100 | 25 – 0 = 25 | -50 – 50 = -100 | 50 – 25 = 25 |
B is the greatest.





